Big Integers in Rust

In preparation for our upcoming pilot bootcamp, I've been working on a few programming challenges. Since we're challenging our bootcamp participants to learn a new language as part of this effort, I thought I'd do the same and finally begin exploring Rust.

One of the simple challenges we introduce in Week 1 is to write a program that calculates the factorial of a given number. A simple program. But we ask that participants consider the following questions:

• For a function factorial(n), how big a value of n can your code handle before it fails?
• How long does it take to run?
• When it does fail, why?

The intention of this simple exercise is to get participants exploring the limitations and boundaries of a given language. For example, when I do this same problem in Python, I can calculate the factorial of n=998 before I run into a "recursion depth exceeded" error.

Understanding Language Boundaries

It would be easy to let this slide and just say "Okay, Python can't handle those large factorials". But my curiosity got the better of me. Why 998 and not 1000? The default recursion limit in Python is 1000.

Python Prototype

My Python code looks like this:

import sys 

def main():
    N = int(sys.argv[1])
    print(f'factorial({N}) = {factorial(N)}')
    

def factorial(n):
    if n == 0 or n == 1:
        return 1
    return n * factorial(n-1)


if __name__ == '__main__':
    main()

The answer is actually rather simple. We would actually expect it to fail at 999 not 1000, because we return our base case at n=1. So factorial(1) makes 1 function call, factorial(2) makes 2 function calls, and so on. So factorial(999) makes 999 function calls. But we also call the main function. So we exceed the limit of 1000 function calls.

Rust Prototype

Our rust code is not that dissimilar:

fn main() {
    let args: Vec<String> = std::env::args().collect();
    let n = args[1].parse::<i32>().unwrap();
    println!("factorial({}) = {}", n, factorial(n));
}

fn factorial(n: i32) -> i32 {
    if n == 0 || n == 1 {
        return 1;
    }
    return n * factorial(n - 1);
}

Let's run it and see what happens:

Shell

> target/debug/factorial 12
factorial(12) = 479001600
> target/debug/factorial 13
thread 'main' panicked at 'attempt to multiply with overflow', src/main.rs:12:12
note: run with `RUST_BACKTRACE=1` environment variable to display a backtrace

We fail at only n=12. What's going on here? It's a simple as not having enough bits to represent the number. The i32 type is a 32-bit signed integer. The largest number we can represent with 32 bits is 2^31 - 1 or 2147483647. If we change the type, we should be able to get a bit further.

Pushing Language Boundaries

To begin making this more robust, we can use the u64 type instead of i32. This gives us

fn main() {
    let args: Vec<String> = std::env::args().collect();
    let n = args[1].parse::<u64>().unwrap();
    println!("factorial({}) = {}", n, factorial(n));
}

fn factorial(n: u64) -> u64 {
    if n == 0 || n == 1 {
        return 1;
    }
    return n * factorial(n - 1);
}

Now, we can compute much larger numbers

Shell

> target/debug/factorial 13
factorial(13) = 6227020800
> target/debug/factorial 20
factorial(20) = 2432902008176640000
> target/debug/factorial 21
thread 'main' panicked at 'attempt to multiply with overflow', src/main.rs:12:12
note: run with `RUST_BACKTRACE=1` environment variable to display a backtrace

Well ... maybe not much larger. We now overflow at 21. So we can try u128. Again, we update our code to change u64 to u128.

Shell

> target/debug/factorial 30
factorial(30) = 265252859812191058636308480000000
> target/debug/factorial 35
thread 'main' panicked at 'attempt to multiply with overflow', src/main.rs:12:12
note: run with `RUST_BACKTRACE=1` environment variable to display a backtrace

Again, we get a bit further, but not nearly as far as we got with Python. Why is that? Well, Python's built-in int type is actually a variable-length integer. It can grow to whatever size it needs to. In other words, we can represent arbitrarily large integers in Python. It turns out we can do the same in Rust.

Rust BigUint

To push the limits on this, we need to go beyond primitive types. In this case, we introduce the num_bigint crate. This crate provides a BigUint type that allows us to handle arbitrarily large integers.

use num_bigint::BigUint;

fn main() {
    let args: Vec<String> = std::env::args().collect();
    let n = args[1].parse::<usize>().unwrap();
    println!("factorial({}) = {}", n, factorial(n));
}

fn factorial(n: usize) -> BigUint {
    if n == 0 || n == 1 {
        return BigUint::from(1u32);
    }
    return n * factorial(n - 1);
}

There are still some limitations. For example, the bigger the numbers get, the longer it takes the BigUint type actually perform the multiplication. The highest I tested this was factorial(50000), which took about 11.8s on my 8-Core Intel i9.

Pushing Python

To compare the Rust performance to the Python example, we use the Unix time command. We can increase Python's recursion limit using the sys.setrecursionlimit() function.

Running our python code again factorial.py 50000 produced something I didn't expect from Python: a seg fault. In fact with a bisection search, we narrow down exactly when this happens:

Shell

> time python factorial.py 38824
Segmentation fault: 11

This is something we could dive way deeper into. In the interest of brevity and staying on topic, I'll save that for another post. This StackOverflow post has some information that might be useful if you're interested exploring this path yourself.

Benchmarking Rust vs. Python

Finally, I compared the times of the Python code to the Rust implementation as was shocked by what I found.

Language	N	Time
Python	10000	0.155s
Rust	10000	0.434s
Python	20000	0.230s
Rust	20000	1.715s
Python	30000	0.444s
Rust	30000	4.077s

This would seem to imply that Python is more performant than Rust. Much more performant. As a new user of Rust, it might be easy to accept that as the conclusion. However, the default cargo build command for Rust builds a debug version of the code.

To build a production release (i.e. without a bunch of debug information in it), we need to run cargo run build --release. This produces a binary that is much more performant. To show this, the plot below shows the performance of the Python code, the Rust code (built in debug mode), and the Rust code built in release mode.

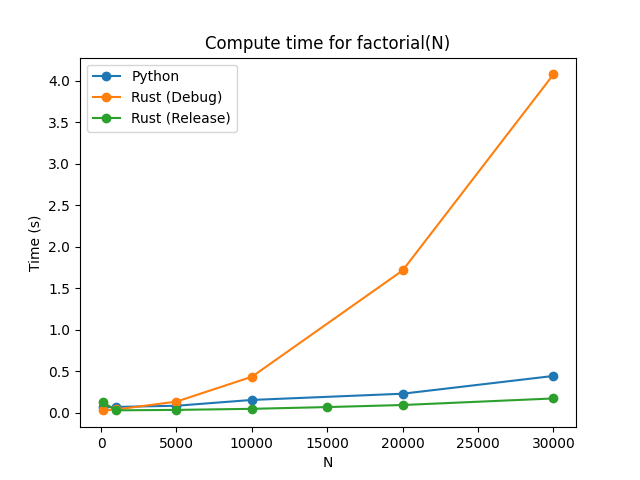
With this, it becomes much clearer that the Rust code is actually much more performant than the Python code.